첫번째 글엔 라플라스 변환 테이블만 올려놓고 그냥 외우는게 낫다고 했는데
설명을 붙이는 걸 깜빡했다.
여기서 라플라스 변환의 쓰임은 크게 두 가지로 나뉘는데
첫번째는 알다시피 미분방적식을 풀 때 필요하고
두번째는 복잡한 미분방적식을 하나의 input 과 하나의 output의 관계식으로 나타내게 할 수 있다.
지금 우리에게 필요한 건 두번째이다. 이걸 transfer function 이라고 하는데 (네이버에 검색해보니 전달함수라고 함.)
이 transfer function은 input과 output의 관계식을 나타낸 것인데,
몇 가지 조건이 있다.
transfer function은 output/input 이고 어떤 형태의 input인지 상관이 없다.
또한 모든 initial condition은 0으로 가정하며
transfer function 안에 input 과 output이 있어서는 안된다.
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ4/2/2017 추가ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
그리고 선형이면서 시간에 따라 변화되지 않아야 한다. (Linear Time Invariant)
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
그래서 라플라스 변환에 대해 깊이 안 들어간거고 그냥 테이블이나 외우는 게 낫다고 한 것이다.
어차피 하나하나 계산하느니 테이블보고 적는게 몇 배는 빠름.
그럼 다음으로 넘어가자.
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
시스템 컨트롤을 배워야하는데
시스템 컨트롤을 배우기 위해선 당연히 시스템 모델링하는 방법에 대해서 알아야한다.
시스템 모델링의 가장 기본은 스프링과 댐퍼를 이용한 모델링인데
여기 내 블로그에서는 기본적으로 이상 스프링과 댐퍼를 쓸 것이다.
이상 스프링의 경우엔,
1. 선형이다
2. 무게가 없다
3. 에너지를 발산하지 않는다
이상 댐퍼의 경우엔,
1. 선형이다
2. 무게가 없다
3. 에너지를 보존하지 않는다
그리고 가장 기본적인 질량도 빼먹으면 안된다.
그럼 이제 질량, 스프링, 댐퍼의 기본 식을 알아보자.
질량은 뉴턴의 제 2법칙인 F = ma 식을 사용한다.
스프링은 훅의 법칙인 F= kx 식을 사용한다.
댐퍼는 속도에 비례하기에 F = b dx/dt 식을 사용한다.
역시 직접 해봐야 훨씬 이해가 빠를 것이다.

이렇게 스프링-댐퍼 모델이 있다고 하자.

이 모델에 힘 F 가 가해진다고 하자.

그럼 가장 먼저 FBD 를 그려보는데 스프링과 댐퍼의 힘 방향이 왜 F 의 반대냐하면,
힘 F가 가해지다가 갑자기 뿅 없어진다고 해보자. 그럼 질량 m은 어느 방향으로 갈까?
그러하다. 당연히 반대방향으로 움직일 것이다. 고로 반대방향임. 많이 하다보면 알게 됨.
아무튼, x 와 y 의 방향을 정하고 뉴턴의 제 2법칙인 F = ma를 이용해 각 방향의 힘의 합을 구해보자.

y 방향으로 가해지는 힘이 없기에 합은 당연히 0 이다.

x 방향은 가해지는 힘이 많다!
가속도 a 는 거리 x 의 두 번 미분한 값이고
속도 v 는 거리 x 의 미분한 값인건 알고 있을테니
x 로 표기하겠다. 그리고 이렇게 하는게 상당히 편함 나중에.
F_x 의 식을 잠깐 변형해 보자면

이렇게 나타낼 수가 있다. 이 시스템의 전달함수를 구해보자.
그렇다면 라플라스 테이블을 보고나서 적용이 가능한 걸 찾아야하는데
37번이 딱 알맞아 보인다.

37번을 적용해보면
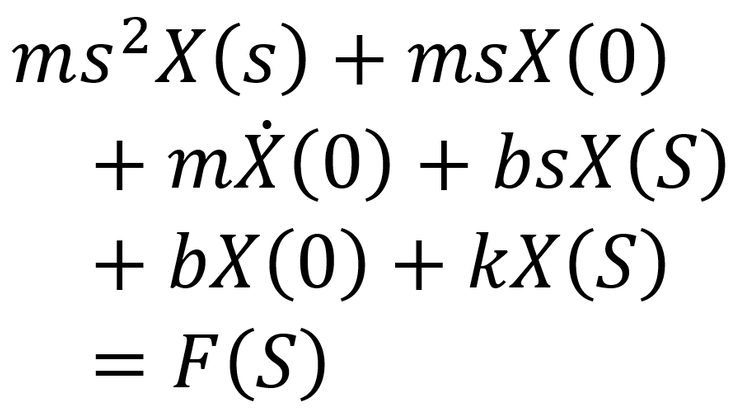
이렇게 식이 나오는데 전달함수의 모든 initial condition은 0으로 가정하기에
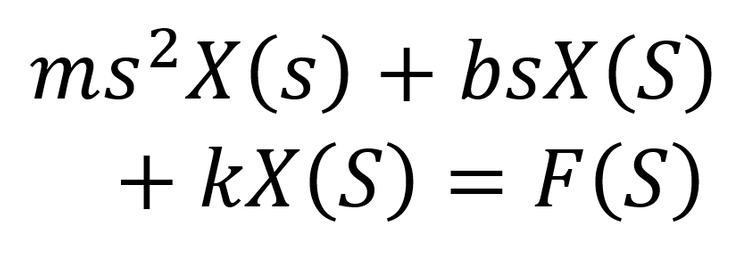
이렇게 깔끔하게 정리가 가능하다. 그리고 이 식을 다시 변형시켜보면

이런 식으로 바꿀 수가 있는데 위에보면 전달함수는 output/input 으로 나타낼수 있다고 적어놓았다.
FBD 을 보면 input은 힘 F 이고 output은 F의 따른 x의 변화인데
그렇다면 이 시스템의 전달함수는 X/F 가 되어야한다.
그리고 [ms^2 + bs + k] 와 F(S) 를 양 변에 나눠주면 X/F의 형태가 나오게 된다.

쨘.
이 시스템의 전달함수는 1/ms^2+bs+k 가 된다.
왜 이런 짓을 해야하는지 의문이 들 수도 있겠는데 input과 output의 관계를 아는 건 정말로 중요하다.
왜냐면 이 식을 이용해서 여러가지를 알아낼 수 있기 때문이다.
오늘은 여기까지만 적고 내일은 오늘 깜빡하고 넘어간 DOF 와 system order를 하고 다른 필요한 걸 해야겠다.
'System Control' 카테고리의 다른 글
| Frequency Response (0) | 2020.07.10 |
|---|---|
| Transient Response 두 번째 (0) | 2020.07.10 |
| Transient Response (0) | 2020.07.10 |
| DOF/System Order (0) | 2020.07.10 |
| 라플라스 변환 (0) | 2020.07.10 |




댓글