Transient Response 두 번째
저번에 transient response 에 대해서 적었었는데,
이번에도 transient response 에 대해서 적을 것이다.
저번 글과 이번 글의 다른 점은
저번 글은 1st order system 에 대한 transient response 였다면,
이번 글은 2nd order system 에 대한 transient response 이라는 것.
Transient Response
오랜만에 글을 쓴다. 이번엔 Transient response (네이버 검색해보니 과도 응답 이라고 나옴) 에 대해서 알아보자. Transient response 는 시스템의 시간이 지남에 따라 반응하는 걸 뜻한다. 예를 들면 스프
honour.tistory.com
위에 링크를 보면 내가 DOF 와 system order에 대해서 간략하게 설명하는 글을 적었었는데
여길 보면 1st order 와 2nd order 시스템의 차이점을 적어놨다.
다시 요약해서 적어보자면
1st order system = 특정한 input이 아니면 진동 (Oscillation) 이 절대로 없다.
2nd order system = 무조건 적으로 진동하진 않지만 진동할 가능성을 가지고 있다.
그럼 저번 글엔 1st order system 의 transient response 를 알아보았으니
이번엔 2nd order system 의 transient response 를 알아보자.

먼저 이런 스프링-댐퍼 시스템이 있다고 하자. 이 시스템은 1 DOF 2nd order 이다.

FBD 를 그리고 전달함수 (Transfer Function) 를 구해보자.

전달 함수 구하는 방법은
시스템 모델링
첫번째 글엔 라플라스 변환 테이블만 올려놓고 그냥 외우는게 낫다고 했는데 설명을 붙이는 걸 깜빡했다. 여기서 라플라스 변환의 쓰임은 크게 두 가지로 나뉘는데 첫번째는 알다시피 미분방적
honour.tistory.com
요기로 가면 나온다.
그럼 이번엔 이 전달 함수의 eigenvalue 를 구해보자.
1st order 는 eigenvalue 가 하나라서 그냥 풀면 되지만 2nd order 는 eigenvalue 가 두 개이다.
그래서 필요한 건 근의 공식. 2차 방정식을 풀듯이 풀면 된다.
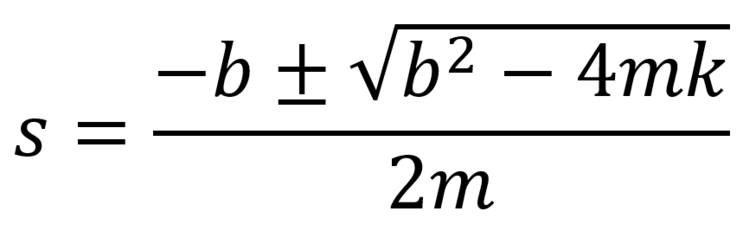
그렇다면 두 개의 eigenvalue 의 값은 각각


이렇게 나온다.
여기서 중요한 것은 판별식.

알다시피 판별식은 3가지의 가능성을 가지고 있는데,
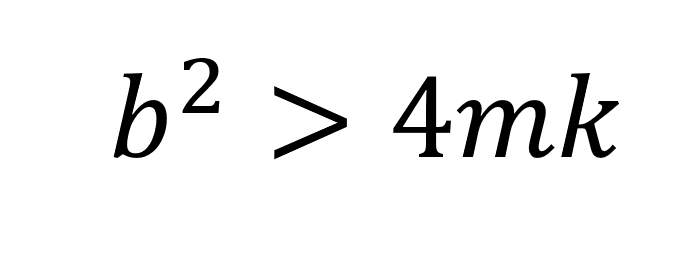
Case 1.
b 제곱이 4mk 보다 클 때.

Case 2.
b 제곱이 4mk 와 같을 때.

Case 3.
b 제곱이 4mk 보다 작을 때.
Case 1 부터 차근차근 보자.
b 제곱이 4mk 보다 크면 루트 안의 값은 + 가 된다.
그렇다면 eigenvalue 의 값은 모두 정수가 된다.
b 제곱이 4mk와 같으면 루트 안의 값은 0이 된다.
그렇다면 eigenvalue 의 값은 모두 같다.
b 제곱이 4mk 보다 작으면 루트 안의 값은 - 가 된다.
그렇다면 eigenvalue 의 값은 모두 복소수가 된다.
조금 더 나가기전에 잠깐 Case 1을 봐보자.
Case 1의 경우, 두번째 eigenvalue 의 경우엔 무조건 - 가 되니까 문제가 없는데
첫번째 eigenvalue 의 경우엔 eigenvalue 가 + 가 될 가능성이 있다.
이제 와서 생각해보니 eigenvalue 가 - 여야하는 이유를 설명하지 못했다.
Eigenvalue 가 - 여야 하는 이유를 간략하게 설명하자면

속도 v = Ae^st 인데, 여기서 s 가 바로 eigenvalue 이다.
만약에 이 s 값이 + 라면 시간이 지날수록 속도가 올라가는 기이한 현상이 일어나게 된다.
고로 Eigenvalue 는 - 여야함.
물론 나중에가면 eigenvalue 가 + 인 시스템도 다룰 예정이다.
하지만 지금 당장은 eigenvalue 가 - 여야 정상적인 시스템이라는 걸 알아두면 좋겠다.
s < 0 -> 정상적인 시스템
s > 0 -> 비정상적인 시스템
다시 본론으로 넘어가서,
Case 1을 보면 eigenvalue 가 + 일 가능성이 있는데 한 번 실제로 해보자.
첫번째 eigenvalue 식을 풀어보면..



고로 -b/(2m) + sqrt((b/(2m))^2 - (k/m)) < 0 이 되기 위해선
b, k, m 중 하나가 - 여야만 가능하다.
하지만 알다시피 그것은 불가능하기에 모든 eigenvalue 의 값은 0 보다 작을 수 밖에 없다.
그렇다면 위의 시스템을 MATLAB을 이용해서 한 번 돌려보자.
먼저 Case 1 일 때.
F = 1
m = 1
b = 0.7
k = 0.1
이라고 임의로 수를 넣어서 돌려보면

이렇게 나온다.
그리고 eigenvalue 를 계산해보면 각각 s = -1, -0.4 가 나온다.
Case 2 일 때.
F = 1
m = 1
b = 0.7
k = 0.1225
라고 수를 넣어보면

이렇게 나온다.
그리고 eigenvalue 를 계산해보면 각각 s = -0.7, -0.7 이 나온다.
그럼 마지막으로 Case 3 일 때.
F = 1
m = 1
b = 0.7
k = 0.5
라고 수를 넣어보면

이렇게 나온다.
그리고 eigenvalue 를 계산해보면 각각 s = -0.7000 - 1.2288i , -0.7000 + 1.2288i 가 나온다.
Case 1 과 2는 마치 저번 글에서 봤었던 그래프랑 상당히 유사하다.
하지만 Case 3은 확연히 차이가 난다.
그래프를 보면 알겠지만 Case 3의 경우엔 시스템이 진동을 한다.
그리고 전에 썼던 DOF/System order 글을 보면
2nd order 은 진동 가능성을 가지고 있다 라고 적어놨는데 그게 바로 이때,
eigenvalue 가 복소수일 때 시스템은 진동을 한다.
그럼 마지막으로 두 개의 eigenvalue 의 차이가 엄청나다면 어떻게 될까?
두 eigenvalue 의 차이가 큰 2nd order와 1st order를 비교해보자.
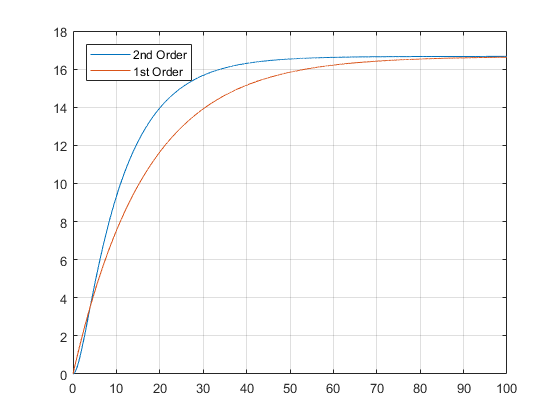
이렇게 나온다.
보다시피
1st order 와 2nd order 가 거의 비슷하다.
결론을 내려보면
두 eigenvalue 의 차이가 크다면 1st order와 비슷한 반응을 보인다.
Case 2의 경우엔 두 eigenvalue 의 값이 같은데 그렇다고 해서 시스템을 1st order 로 만들지 않는다는 점도 알아두면 좋다.
정리하자면
b^2 > 4mk -> Overdamped
b^2 = 4mk -> Criticallydamped
b^2 < 4mk -> Underdamped
이며
s1 >>>>>>>>>> s2 라면 1st order 시스템에 가까워진다.